This is a tour of some curiosities I unearthed and collected from the internet.
Prepared for a Fin Engineering Lunch + Learn,
presented on 14 Apr 2017.
→
Exhibit W
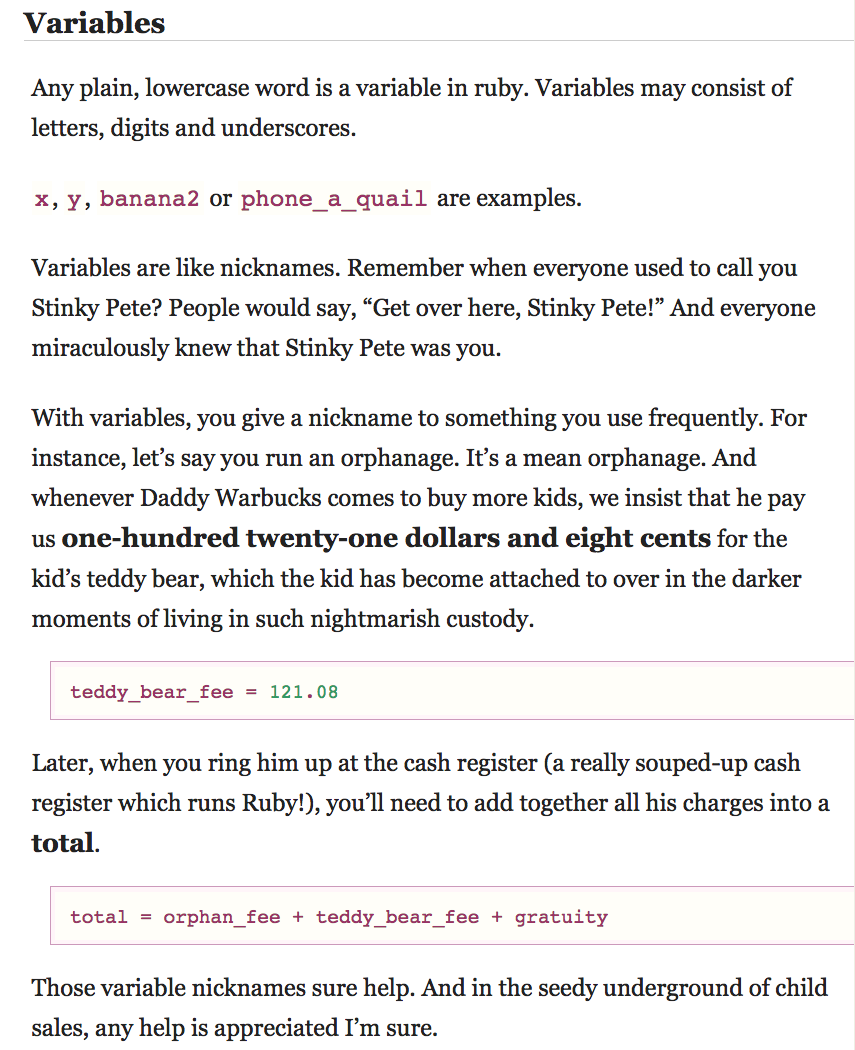
This lunch + learn is dedicated to the only book on programming I have ever fully read.
Here is a sample.


→
Exhibit -
You’ll often hear me ranting about how “the internet is broken.”
→
“Unfollow all your Facebook friends.”
→
“You need to switch your iPhone to Grayscale Display.”
→
“Baby photos are the new cigarettes.”
→
Exhibit 3
I was running down Mandela Parkway the other day and I saw little 3-legged doge.
Whenever I see a 3 legged dog, I always thinks it’s kind of remarkable how happy and playful they look.
→
Exhibit ½ Full
Anyway, seeing this dog got me thinking,
Let’s do something a little more upbeat!
And put the love back in this love/hate relationship I have with the internet…
→
Exhibit Ð

What’s more upbeat than Dogecoin?
Dogecoin is an open source peer-to-peer digital currency, favored by Shiba Inus worldwide. Dogecoin is an open source peer-to-peer digital currency, favored by Shiba Inus worldwide.
The Dogecoin network was originally intended to produce 100 billion Dogecoins, but later, it was announced that the Dogecoin network would produce INFINITE Dogecoins.
– Wikipedia (emphasis mine)
A joke currency that reaches a capitalization of $60M (Jan 2014) represents everything I love about the internet.
And I’ve always wanted to learn about it… 🤔
→
[Archaeological Tools]
🐍 python
→
Exhibit ★
Let’s begin with an investigation of the etymology of the word doge.
Anyone recognize this specimen?

→
Exhibit O.D.

→
Meme Etymolgy ✅… now what about this cryptocurrency bit?
Surprisingly, there is no Dogegoin whitepaper, so I decided to finally read the:
Tons of people sent this to me in my Venmo days, but I never got to it, because we were trying to do the centralized thing, not the decentralized thing…
→

→
“Transactions that are computationally impractical to reverse would protect sellers from fraud, and routine escrow mechanisms could easily be implemented to protect buyers.”
I can transfer value to you by publishing a transaction to the public ledger, and by signing a hash of the transaction and your public key.
But how do you know I did not double spend the coin I am transferring to you without a centralized authority?

You prevent double spending by publishing a timestamp with every transaction, and only accepting the first time a payor spends a coin.
→
HashOf(Data, Timestamp)
Now, we need a distributed timestamp server.


To implement a distributed timestamp server on a peer-to-peer basis, we will need to use a proof- of-work system
→
↱ The Hashcash Cost Funtion
Before we get to how / why we use the proof of work to implement the timestamp server, let’s take quick detour to look at the method we’ll use.
It is based on the:
The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the hash begins with a number of zero bits. The average work required is exponential in the number of zero bits required and can be verified by executing a single hash.
Hashcash was originally proposed as a mechanism to throttle systematic abuse of un-metered internet resources such as email, and anonymous remailers in May 1997.
The basic idea is that a Server generates a Challenge and sends it to a Client that wants to communicate with it.
The Client must compute a Token using an expensive Mint function in order to respond to the Challenge.
The Server than verifies Token with a cheap Value function.
→
Here is what hashcash looks like in python.
Sidebar...
why not learn about @contextmanager? Also,
nmap <Leader>e :!%:p<CR>
from contextlib import contextmanager
import hashlib
import time
@contextmanager
def timer(prefix=""):
'''Time a block of code.'''
start = time.time()
start_c = time.clock()
try:
yield
finally:
end = time.time()
end_c = time.clock()
elapsed = float("%.3f" % (end - start))
elapsed_c = float("%.3f" % (end_c - start_c))
print('{0}: seconds: {1} (wall)'.format(prefix, elapsed))
print('{0}: seconds: {1} (clock)'.format(prefix, elapsed_c))
def sha_as_bin_string(b):
'''
A helper guy to get the SHA-256 hash of a number, b, and return
the hash in a string of 1's and 0's representing it's binary value.
You can essentially just think of this as our sha256.
'''
return "{0:b}".format(int(hashlib.sha256(b).hexdigest(),
16)).rjust(256, '0')
def server_generate_challenge():
'''Just generate a random string.'''
return 'quip modest'
# This grows more and more expensive to compute as
# we grow w (the number of leading zeroes desired)!
def client_mint_token(payload, challenge, w):
token = 0
l = '0' * w
while 1:
if sha_as_bin_string(payload + challenge + str(token)).startswith(l):
break
token = token + 1
return str(token)
def server_check_value(payload, challenge, token, w):
'''Assert Hash of payload + token has desired zeroes.
Always cheap.'''
l = '0' * w
return sha_as_bin_string(payload + challenge + token) \
.startswith(l)
tuples = []
payload = 'marketing spam!'
challenge = server_generate_challenge()
print 'Server Challenge:', challenge
desired_zeroes = [16, 18, 20]
for w in desired_zeroes:
with timer("mint (w={0})".format(w)):
token = client_mint_token(payload, challenge, w)
tuples.append([w, token])
> Grows exponentially more expensive
> mint (w=16): seconds: 0.554 (wall)
> mint (w=18): seconds: 1.607 (wall)
> mint (w=20): seconds: 6.071 (wall)
>
> mint (w=16): seconds: 0.53 (clock)
> mint (w=18): seconds: 1.534 (clock)
> mint (w=20): seconds: 5.656 (clock)
for t in tuples:
with timer("check (w={0})".format(t[0])):
server_check_value(payload, challenge,
t[1], t[0])
> Always cheap
> check (w=16): seconds: 0.0 (wall)
> check (w=18): seconds: 0.0 (wall)
> check (w=20): seconds: 0.0 (wall)
→
Back to Bitcoin
So proof of work is preventing this attack:
I publish a transaction
send coin 123 to YOU
with timestamp 300pm on 14 Apr 2017
Then, later, I try to publish a transaction
send same coin 123 to UNCLE FREDDIE
with timestamp 259pm on 14 Apr 2017
Requiring proof of work on every transaction makes the second transaction far to expensive for me to compute because:
To modify a past block, an attacker would have to redo the proof-of-work of the block and all blocks after it and then catch up with and surpass the work of the honest nodes.
If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains.
→
But wait…
An attacker with sufficient resources could launch a large-scale parallel attack by building hundreds or even thousands of implementations of the algorithm in hardware and having each search a different subset of the key space. This divides the amount of time needed to complete a brute-force attack by the number of implementations available, very possibly bringing it down to a reasonable time frame.
→
My MacBook has multiple processors (I think).
$ sysctl -n hw.ncpu
4
$ sysctl hw.physicalcpu
hw.physicalcpu: 2
NICE.
→
Let’s look at a rudimentary parallelization in python.
from multiprocessing import Pool
import multiprocessing
# Pass in an initial token value, and step to parallelize search across
# mulitple processors
def client_mint_token_mp(payload, challenge, w, token=0, step=4):
start = time.time()
start_c = time.clock()
l = '0' * w
while 1:
if sha_as_bin_string(payload + challenge + str(token)).startswith(l):
break
token = token + step
end = time.time()
end_c = time.clock()
elapsed = float("%.3f" % (end - start))
elapsed_c = float("%.3f" % (end_c - start_c))
prefix = 'parallelized mint (w={0})'.format(w)
print('{0}: seconds: {1} (wall)'.format(prefix, elapsed))
print('{0}: seconds: {1} (clock)'.format(prefix, elapsed_c))
return str(token)
w = 20
def search_shard(shard_number):
return client_mint_token_mp(payload, challenge, w, shard_number, 4)
found_the_treasure = 'Nope'
pool = Pool()
for token in pool.imap_unordered(search_shard, range(4)):
found_the_treasure = token
# as soon as we find a working solution,
# we can abort searching the other shards
multiprocessing.pool.Pool.terminate(pool)
break
> parallelized mint (w=20): seconds: 3.087 (wall)
> cf. on a single processor 6.071
>
> parallelized mint (w=20): seconds: 1.742 (clock)
> cf. on a single processor 5.656
NICE.
→
Dogecoin Uses scrypt
Dogecoin is based on Luckycoin, which features a randomized reward that is received for mining a block, although this behavior was later changed to a static block reward in March 2014.
Luckycoin is based on Litecoin: uses scrypt technology in its proof-of-work algorithm. The use of scrypt means that miners cannot use SHA-256 > bitcoin mining equipment, and that dedicated FPGA and ASIC devices used for mining are complicated to create.
Wow! Dogecoin sounds like Dogecoin is more secure?
Much safe.
→
Exhibit 🤓
Another detour to another whitepaper!
Widely used key derivation functions have thus far used constant amounts of logic and memory; in order to increase the cost of a parallel attack, we would like to parameterize not only the operation count, but also the memory usage.
Memory is the computationally usable resource general-purpose computers have which is most expensive to reproduce in hardware.
A memory-hard algorithm is an algorithm which asymptotically uses almost as many memory locations as it uses operations.
A sequential memory-hard function is one where not only the fastest sequential algorithm is memory-hard, but additionally where it is impossible for a parallel algorithm to asymptotically achieve a significantly lower cost.
Eh, can we just see some code?
→
A sequential memory-hard function… ROMix
def one_dumb_hash(x):
"""In the-real-scrypt, this is Salsa20/8"""
return list(reversed(x))
def integerify(B):
"""
Treat an array of 0,1 as a representation of an integer in
binary and return an int.
"""
return int("".join([str(b) for b in B]), 2)
def ROMix(H, Integerify, B, N):
"""
H - A hash function.
where k = Length of output produced by H
B - Input of length k bits. (array of [0,1 ...])
Integerify - A bijective function from { 0, 1 }^k to { 0,.. 2^k-1 }
N - Integer work metric, < 2k/8
pseudo-python for ROMix from
https://www.tarsnap.com/scrypt/scrypt.pdf
"""
k = len(B)
assert N < 2 * k / 8, "N must be < 2 * len(B) / 8"
X = B[:] # make a copy
# create another array to hold our large number of 'random' values.
# This is what makes this memory-expensive.
V = [0 for x in xrange(0, N)]
for i in xrange(0, N):
V[i] = X
X = H(X)
for i in xrange(0, N):
j = Integerify(X) % N
# xor X with V[j]
for p in xrange(0, len(X)):
# We need all of V in memory for every iteration,
# because the index j is random.
X[p] ^= V[j][p]
X = H(X)
return X
# Chceckout an actual scrypt implementation in python here:
# https://github.com/ricmoo/pyscrypt/blob/master/pyscrypt/hash.py
→
PROOF!
The scrypt paper has this nice proof demonstrating the cost of the function:

… eh, let’s leave that for another day.
→
Final Detour! ↝ ↩ ↬ ↭ ↷
↯ Binomial Random Walk ↯
→
X X X
Better…
→
⇝ Gambler’s Ruin Problem ⇝
→
X X X
Better…
→
⇩ From the scrypt whitepaper… ⇩
good old Bernstein...
However, as Bernstein famously pointed out in the context of integer factorization [10], while parallelized hardware implementations may not change the number of operations performed compared to software implementations, this does not prevent them from dramatically changing the asymptotic cost, since in many contexts — including the embarrassingly parallel task of performing a brute-force search for a passphrase — dollar-seconds are the most appropriate units for measuring the cost of a computation.
What is this [10]?
→
📘Circuits for Integer Factorization: A Proposal
→
The Snakelike Order
One of the few things I was able to grasp well enough for lunch + learn in a cursory exploration of Bernstein’s whitepaper was Schimmler Sorting.
Schimmler’s algorithm sorts m2 numbers in 8m - 8 steps on a two dimensional machine of size m2, where m is a power of 2.
It relies on special hardware (a 2 dimensional machine consisting of a m x m mesh of m2 cells, each cell holding one number and each cell connected to the adjacent cells), and depends upon odd-even-transposition sorting:

Here is what Schimmler Sorting looks like in an 8x8 mesh:
Given:
3 1 4 1 5 9 2 6
5 3 5 8 9 7 9 3
2 3 8 4 6 2 6 4
3 3 8 3 2 7 9 5
0 2 8 8 4 1 9 7
1 6 9 3 9 9 3 7
5 1 0 5 8 2 0 9
7 4 9 4 4 5 9 2
Sort the quadrants:
1 1 2 3→ →2 2 2 3
3 3 3 3→ →4 5 5 6
3 4 4 5→ →6 6 7 7
5 8 8 8→ →9 9 9 9
1 1 0 0← ←2 2 1 0
4 4 3 2← ←5 4 4 3
7 6 5 5← ←9 8 7 7
9 9 8 8← ←9 9 9 9
Sort the columns,
top to bottom:
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
1 1 0 0 2 2 1 0
1 1 2 2 2 2 2 3
3 3 3 3 4 4 4 3
3 4 3 3 5 5 5 6
4 4 4 5 6 6 7 7
5 6 5 5 9 8 7 7
7 8 8 8 9 9 9 9
9 9 8 8 9 9 9 9
Sort the rows,
snakelike:
0 0 0 1→ →1 1 2 2
3 2 2 2← ←2 2 1 1
3 3 3 3→ →3 4 4 4
6 5 5 5← ←4 3 3 3
4 4 4 5→ →6 6 7 7
9 8 7 7← ←6 5 5 5
7 8 8 8→ →9 9 9 9
9 9 9 9← ←9 9 8 8
Sort the columns,
top to bottom:
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
0 0 0 1 1 1 1 1
3 2 2 2 2 2 2 2
3 3 3 3 3 3 3 3
4 4 4 5 4 4 4 4
6 5 5 5 6 5 5 5
7 8 7 7 6 6 7 7
9 8 8 8 9 9 8 8
9 9 9 9 9 9 9 9
Sort the rows,
left to right:
0 0 0 1→ →1 1 1 1
2 2 2 2→ →2 2 2 3
3 3 3 3→ →3 3 3 3
4 4 4 4→ →4 4 4 5
5 5 5 5→ →5 5 6 6
6 6 7 7→ →7 7 7 8
8 8 8 8→ →8 9 9 9
9 9 9 9→ →9 9 9 9
CRAZY.
→
Speaking of CRAZY

so speed.
→
Isn’t this just a different kind of baby photo?
While I was working on this lunch + learn, I got to thinking, why is it that I like Dogecoin?
It’s kind of vulgar and shares a lot in common with things I really don’t like about the internet.
→
But there is an absurdity and whimsical-ness that I think is the root of my interest.
→
Dogecoin is a reminder that all currency is a fiction / construct manifested by society.
→
The New Aesthetic
This introspection about doges and computation then got me thinking about the New Aesthetic.
A basic idea of the New Aesthetic is that glitches, machine generated images, memes, and digital popart all create the sense of machines smiling back at us.
These images or memes are not so much the product of the agency of any individual human actor so much as they are the ouput of the rules of a system human actors are operating within.
The New Aesthetic, then, can be understood as a comportment towards “seeing” computation, responding to it, or merely being correctly attuned to it (in a subsequent chapter this is explored due to its potential for the pacification of the user).
…
Pareidolia involves seeing importance in vague and random phenomena, for example a face in a random collection of dots on paper. The term ‘digital pareidolia’ we coin to gesture towards this tendency in the New Aesthetic to see digital causes for things that happen in everyday life.

→
“cool, weird, provocative, suggestive, otherworldly, but also impoverished”
[The New Aesthetic makes the claim] “This is how contemporary reality looks to our pals, the visionary machines.” …

If machine vision was our pal, then we wouldn’t need James Bridle to assert that for us. We’d have a Bridlebot, a Googleized visual search-engine that could generate as much aesthetics as we want. That won’t happen. Why not? Because it is impossible. It’s as impossible as Artificial Intelligence, which is a failed twentieth-century research campaign, reduced to a sci-fi conceit.
– Bruce Sterling (2012)
→
Inceptionism / Bridlebot2015
/ Machine Dreams
One way to visualize what goes on is to turn the network upside down and ask it to enhance an input image in such a way as to elicit a particular interpretation. Say you want to know what sort of image would result in “Banana.” Start with an image full of random noise, then gradually tweak the image towards what the neural net considers a banana.
→


→
What next?
→
From Computation to Consciousness
→
QUOD ERAT DEMONSTRANDUM
Questions?
→
FIN.